第15回 平面に目盛られた数
谷口 隆
平面に複素数を目盛るという考え方がある．要点を箇条にすると次の通りだ．
(イ) |
|
$2$ 乗すると $-1$ になるような数 $i$ があると想像する．つまり $i^2$ ＝ $-1$．
|
(ロ) |
|
$x$，$y$ を実数として， $x＋yi$ という形で表される数（＝複素数）の世界を考える．
|
(ハ) |
|
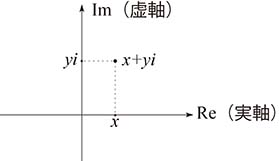
これまで $xy$ 平面上で $(x,y)$ という実数の組を表していた点が， $x＋yi$ という複素数を表していることにする．そのように考えたときの平面を複素数平面という． $x$ 軸を実軸， $y$ 軸を虚軸という．
|
第一印象で物事を判断してはイカンと言われる．しかしこれは，『どう控えめに見積もってもなお，受け入れがたい』――それが“常識的な感覚”ではないだろうか．上記イ・ロ・ハの考え方に習熟し，ひとたび馴染めば，
「実数を直線に目盛って数直線ができる．この考え方をまっすぐに拡張し，複素数を平面に目盛って，複素数平面とするのだ．」
と確信に満ちて話すようになる．でも，初めて知ったときにこんなことを言われても戸惑うばかりだろう．どうすれば，このイ・ロ・ハを真面目に検討してみよう，という積極的な心持ちになれるだろうか．今回は方程式
$x^n$ ＝ $1$
をいくつかの $n$ で考え，解を複素数平面に目盛ってみることで，このとびっきり斬新な着想の端緒を探ってみたい．
◇ ◇ ◇
(a) |
|
手始めに， $4$ 以下の $n$ で $x^n-1$ ＝ $0$ を解いてみよう．
（i） $n$ ＝ $1$ のときは何をするでもなく， $x$ ＝ $1$ が解だ．
（ii） $n$ ＝ $2$ なら $x^2-1$ ＝ $(x-1)$ $(x+1)$ ＝ $0$ から，解は $x$ ＝ $1$， $-1$ となる．
（iii） $n$ ＝ $3$ なら $x^3-1$ ＝ $(x-1)$ $(x^2+x+1)$ ＝ $0$ で， $x$ ＝ $1$ または $x^2+x+1$ ＝ $0$ である．後者は $2$ 次方程式の解の公式から
$x$ ＝ $\dfrac{-1\pm\sqrt{1^2-4}}{2}$ ＝ $\dfrac{-1\pm\sqrt{-3}}{2}$ ＝ $-\dfrac{1}{2}\pm\dfrac{\sqrt{3}}2i$
となって，これと $x$ ＝ $1$ を合わせた $3$ 個が解だ．
（iv） 最後に $n$ ＝ $4$ のときは， $i^2$ ＝ $-1$ に注意して，
$x^4-1$ ＝ $(x^2-1)$ $(x^2+1)$ ＝ $(x^2-1)$ $(x^2-i^2)$
＝ $(x-1)$ $(x+1)$ $(x-i)$ $(x+i)$
だから， $x^4-1$ ＝ $0$ の解は $x$ ＝ $1$ ， $-1$ ， $i$ ，$-i$ の $4$ 個になる．
以上の $n$ ＝ $1$ ， $2$ ， $3$ ， $4$ について， $x^n$ ＝ $1$ の解を複素数平面に目盛ってみよう．
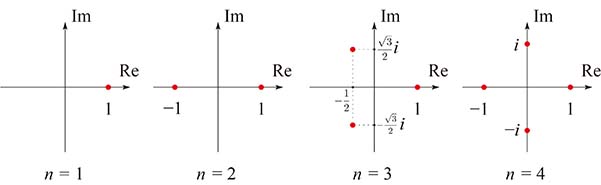
どうだろう．何か規則が見えるだろうか．
|
(b) |
|
もう少し先の $n$ まで進んでみたい．
（i） となるとまずは $n$ ＝ $5$ だが， $x^5$ ＝ $1$ は少し解きにくい．面白い方程式なので補遺で扱うこととし，ここでは $n$ ＝ $6$ に進もう． $x^6-1$ ＝ $(x^3-1)$ $(x^3+1)$ ＝ $0$ から， $x^3-1$ ＝ $0$ または $x^3+1$ ＝ $0$ である．前者は $n$ ＝ $3$ のときそのものだ．後者については $x^3+1$ ＝ $(x+1)$ $(x^2-x+1)$ だから，やはり解の公式から計算できて，$x$ ＝ $-1$ ， $\dfrac12\pm\dfrac{\sqrt3}2i$ と新たに $3$ 個の解が出てくる．
（ii） ほかに解けるケースがあるだろうか． $n$ ＝ $7$ の $x^7$ ＝ $1$ は一筋縄ではいかないが， $n$ ＝ $8$ は手立てがある． $x^8-1$ ＝ $(x^4-1)$ $(x^4+1)$ で， $x^4-1$ ＝ $0$ は $n$ ＝ $4$ で解いたので $x^4+1$ ＝ $0$ を解こう．一計を案じ，
$
\begin{align*}
x^4+1
&=x^4+2x^2+1-2x^2\\
&=(x^2+1)^2-(\sqrt2x)^2\\
&=(x^2+\sqrt2x+1)(x^2-\sqrt2x+1)
\end{align*}
$
と変形すれば， $2$ 次方程式 $2$ 個になる． $x^2-\sqrt2x+1$ ＝ $0$ からは
$x$ ＝ $\dfrac{\sqrt2\pm\sqrt{2-4}}2$ ＝ $\dfrac{\sqrt2\pm\sqrt{2}i}2$ ＝ $\dfrac{1\pm i}{\sqrt2}$
で，同様に $x^2+\sqrt2x+1$ ＝ $0$ からは $x$ ＝ $\dfrac{-1\pm i}{\sqrt2}$ が得られる．
$n$ ＝ $6$， $8$ で $x^n$ ＝ $1$ の解を複素数平面に目盛ってみよう．
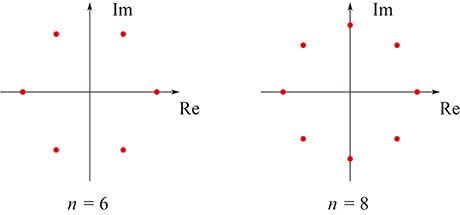
どうだろう．何やら図形が見えないだろうか？――そう， $n$ ＝ $6$ では点を順に結んでいくと正六角形ができる．そして， $n$ ＝ $8$ なら正八角形じゃないか！
|
(c) |
|
ここまでの話（a），（b）をまとめてみよう．（b）の正六角形と正八角形は，いずれも，原点を中心とする半径 $1$ の円（単位円という）に内接している．
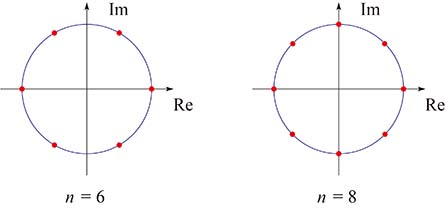
だから，点を結んでいく代わりに単位円を書き，この円周を $6$ 等分， $8$ 等分していると言い換えてもよい．そこで，（a）の $n$ ＝ $1$， $2$， $3$， $4$ でも同じように単位円を書いてみよう．
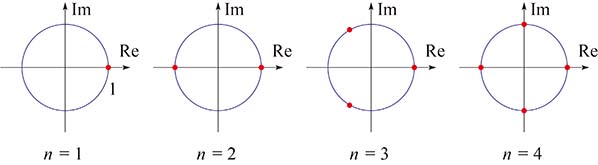
やはり円周を $n$ 等分していることが見て取れる．これだけの $n$ で成り立っているのだから，一般に，
$(\bigstar)$ 『 $x^n$ ＝ $1$ の解 $n$ 個はすべて単位円上にあり，さらにこの円周を $n$ 等分する』
のではないだろうか？と考えることができるだろう．
|
(d) |
|
$(\bigstar)$ を，何かほかの $n$ で検証できないだろうか．座標のことを思い起こすと， $n$ ＝ $9$， $10$， $11$ は簡単でないかも知れないが， $n$ ＝ $12$ だったら計算できるかもしれない．やってみよう． $x^{12}-1$ ＝ $(x^6-1)$ $(x^6+1)$ で， $x^6-1$ ＝ $0$ は $n$ ＝ $6$ のときに解いたので， $x^6+1$ ＝ $0$ を解く． $x^6+1$ ＝ $(x^2+1)$ $(x^4-x^2+1)$ で， $x^2+1$ ＝ $0$ からは $x$ ＝ $\pm i$ が出る． $x^4-x^2+1$ ＝ $0$ の方は $n=8$ のときのやり方をまね，
$
\begin{align*}
x^4-x^2+1
&=x^4+2x^2+1-3x^2\\
&=(x^2+1)^2-(\sqrt3x)^2\\
&=(x^2+\sqrt3x+1)(x^2-\sqrt3x+1)
\end{align*}
$
として解く．複号任意で $x$ ＝ $\pm\dfrac{\sqrt3}2\pm\dfrac12i$ だ．以上出揃った $12$ 個の解を複素数平面に目盛ると $･･････$
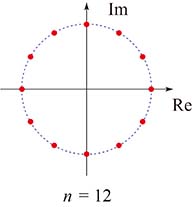
やっぱり， $(\bigstar)$ は成り立っていた！
イ・ロ・ハの考え方には，どうやら何か未知の可能性が秘められているようだ．ここまでくれば，黙って見過ごすには忍びなくなってくるのではないだろうか． $i$ は数直線上にはいなかったが，複素数平面上にちゃんと「いる」のかも知れない．
|
◇ ◇ ◇
$(\bigstar)$ は，ド・モアブルの公式
$(\cos\theta+i\sin\theta)^n$ ＝ $\cos n\theta+i\sin n\theta$
を使うと証明できる．この公式は複素数の冪乗を扱っているが，一般に複素数の加減乗除は，複素数平面で単純明快な解釈がある．今となってはそれは，高校の「数学 III 」で扱われるほどに“常識的な内容”になってしまった．加減乗除や冪乗の段階では，複素数平面を考える積極的な意義はまだやや曖昧だが，そのポテンシャルは垣間見えるだろう．もう一足歩みを進めた複素関数論（本連載第 $5$ 回「素数定理を紐解く〜後編〜」でも紹介した“複素数の微積分”の理論）で，その真価は明らかになる．
この複素数の平面表示は現在では，数学史上の決定的な進歩の一つに数えられている．でも $200$ 年余り時代を遡ると，複素数の立場は数学者の間でもまだまだ不安定だった．ガウスは時代に先んじて平面表示の価値を認識していたが， $1800$ 年ごろのガウスは研究成果を発表するとき，無用の論争を避けるため，複素数平面の思考を表面から消し，多くを実数の言葉に翻訳して発表していた．高校の教科書に複素数平面が載っていることは，人智の大きな進歩であるとともに，人の思い込みの儚さや常識の移ろいを，表すものでもあるのだろう．
（2017/2/1掲載）
（イラスト：マエカワアキオ）
【補遺】
$n=5$ のときの $x^5$ ＝ $1$ を解いてみよう． $x^5-1$ ＝ $(x-1)$ $(x^4+x^3+x^2+x+1)$ だから， $x^4+x^3+x^2+x+1$ ＝ $0$ を解けばよい． $n$ ＝ $8$ のときの技を用いて，
$
\begin{align*}
x^4+x^3+x^2+x+1
&=\left(x^2+\frac12x+1\right)^2-\frac54x^2\\
&=
\left(x^2+\frac{1+\sqrt5}2x+1\right)
\left(x^2+\frac{1-\sqrt5}2x+1\right)
\end{align*}
$
とすると，解を求められる．
$x$ ＝ $\dfrac{-1-\sqrt5}{4}\pm\dfrac{\sqrt{10-2\sqrt5}}4i$ ， $\dfrac{-1+\sqrt5}{4}\pm\dfrac{\sqrt{10+2\sqrt5}}4i$
これと $x$ ＝ $1$ を合わせた $5$ 個が， $x^5$ ＝ $1$ の解だ．
$\cos72^\circ$ ＝ $\dfrac{-1+\sqrt5}{4}$， $\sin72^\circ$ ＝ $\dfrac{\sqrt{10+2\sqrt5}}4$ などから， $x^5$ ＝ $1$ の解が単位円を $5$ 等分していることが分かる．同様の方法で $x^{10}-1$ ＝ $0$ の解を求めることもできて，この場合は解が単位円を $10$ 等分していることが分かる．
（2017/2/1掲載）
※ 次回（第16回）は2017年4月5日（第１水曜日）に掲載いたします．どうぞお楽みに！
ご感想を電子メールでお送りいただければ幸いです．送付先アドレス info@shokabo.co.jp
「数学者的思考回路」 Copyright(c) 谷口 隆，2017
著作権法上の例外を除き，無断で本Webページの全部または一部を転写・複製等することはできません．
（→ 【裳華房】Webサイトのご利用について）
|
